Unlocking The Secrets Of Consecutive Supplementary Angles: A Deep Dive Into Geometry

Rex Haag 14 May 2025

Consecutive supplementary angles are one of those fascinating concepts in geometry that might sound complicated at first, but trust me, they’re not. If you’ve ever wondered about how angles relate to each other in a straight line or how they play a role in solving geometric puzzles, this is the article for you. Whether you’re a student struggling with geometry homework or just someone curious about math, understanding consecutive supplementary angles can open up a whole new world of problem-solving skills.

Geometry isn’t just about shapes and formulas; it’s about understanding the relationships between different parts of a figure. Consecutive supplementary angles are a perfect example of how two angles can work together to form something as simple yet powerful as a straight line. In this article, we’ll break down everything you need to know about these angles in a way that’s easy to follow and super engaging.

But wait, why should you care about consecutive supplementary angles? Well, think about it like this: geometry is everywhere, from the design of buildings to the layout of roads. Understanding how angles interact is not only useful for passing exams but also for appreciating the beauty of mathematics in everyday life. So, let’s dive in and explore this topic together!

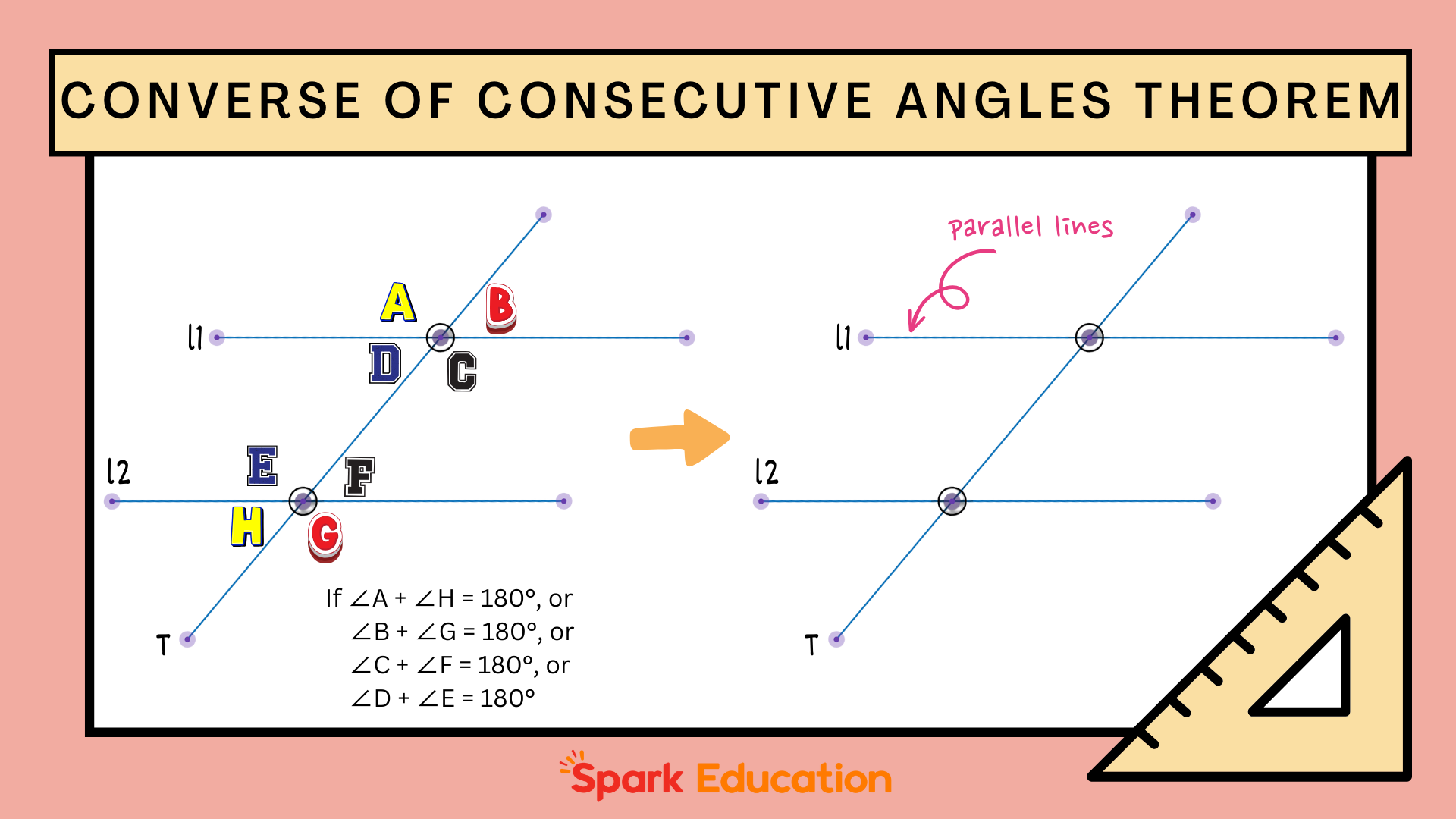
What Are Consecutive Supplementary Angles?

Let’s start with the basics. Consecutive supplementary angles are two angles that are next to each other and add up to 180 degrees. In simpler terms, if you place these two angles side by side, they form a straight line. It’s like when you’re walking and you turn exactly halfway around – you’ve just created a straight angle of 180 degrees!

These angles are called "consecutive" because they are next to each other, and "supplementary" because they add up to 180 degrees. The beauty of geometry lies in how these simple rules can help solve complex problems. Whether you’re dealing with triangles, quadrilaterals, or even circles, understanding consecutive supplementary angles is key to cracking the code.

Key Characteristics of Consecutive Supplementary Angles

Here’s a quick rundown of what makes consecutive supplementary angles unique:

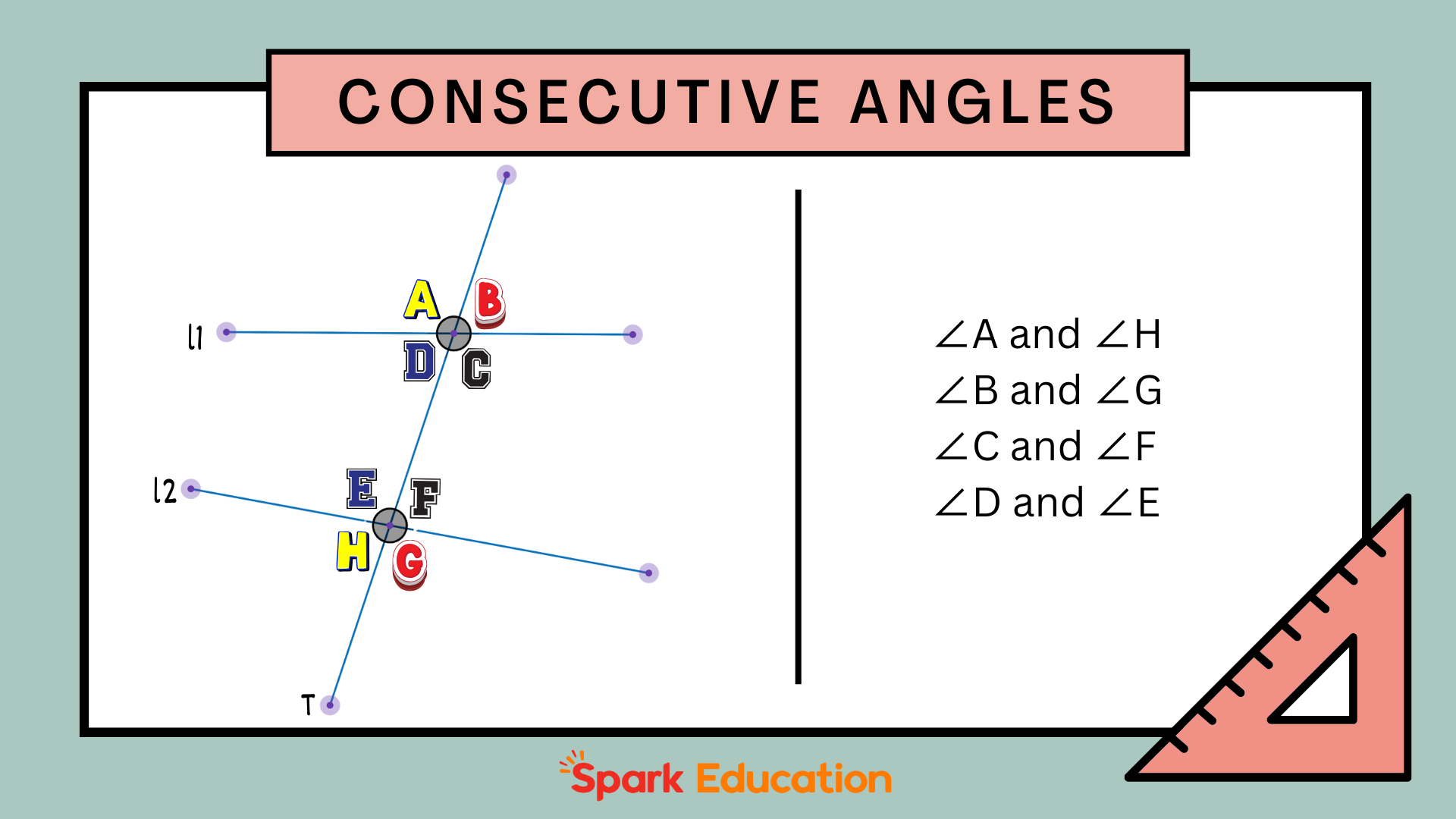
They are adjacent, meaning they share a common vertex and side.
Together, they form a linear pair, which is essentially a straight line.
The sum of their measures is always 180 degrees.
They can be found in various geometric shapes, such as parallelograms and trapezoids.

Understanding these characteristics will help you identify consecutive supplementary angles in any given figure. It’s like having a secret decoder ring for geometry!

Why Are Consecutive Supplementary Angles Important?

Consecutive supplementary angles aren’t just a theoretical concept; they have real-world applications. For instance, architects use these principles to design structures that are both functional and aesthetically pleasing. Engineers rely on them to ensure that bridges and roads are built with precision. Even artists use geometry to create balanced compositions in their work.

But beyond practical applications, learning about consecutive supplementary angles enhances your problem-solving skills. It teaches you to think critically and logically, which are valuable skills in any field. Plus, once you master this concept, you’ll be able to tackle more advanced topics in geometry with confidence.

Real-Life Examples of Consecutive Supplementary Angles

Let’s bring this concept to life with some examples:

Road Intersections: When two roads meet at a straight angle, the angles formed at the intersection are consecutive supplementary angles.
Building Design: Architects often use these angles to ensure that walls and ceilings align perfectly.
Sports: In sports like billiards, players use the concept of supplementary angles to calculate the trajectory of the ball.

As you can see, consecutive supplementary angles are all around us, even if we don’t always notice them. By understanding their role, you’ll start seeing the world through a geometric lens.

How to Identify Consecutive Supplementary Angles

Identifying consecutive supplementary angles might seem tricky at first, but with a little practice, it becomes second nature. Here’s how you can spot them:

First, look for angles that are next to each other and share a common side. Then, check if their measures add up to 180 degrees. If both conditions are met, congratulations – you’ve found a pair of consecutive supplementary angles!

Here’s a tip: Always double-check your calculations. It’s easy to make a mistake when adding angles, so take your time and be thorough. Remember, geometry is all about precision.

Common Mistakes to Avoid

While identifying consecutive supplementary angles, keep an eye out for these common mistakes:

Confusing consecutive supplementary angles with complementary angles (which add up to 90 degrees).
Forgetting to check if the angles are adjacent.
Not verifying that the sum of the angles is exactly 180 degrees.

Avoiding these pitfalls will help you solve problems more accurately and efficiently. Practice makes perfect, so don’t be afraid to try different examples until you feel confident.

Consecutive Supplementary Angles in Geometry Problems

Now that you know what consecutive supplementary angles are and how to identify them, let’s see how they fit into geometry problems. Whether you’re working on a basic worksheet or tackling a complex exam question, these angles can help you find solutions quickly.

For example, consider a problem where you’re given two angles, one measuring 120 degrees and the other unknown. If you know that these angles are consecutive supplementary angles, you can easily calculate the missing angle by subtracting 120 from 180. The answer? 60 degrees. See how simple that was?

Tips for Solving Geometry Problems

Here are some tips to help you solve geometry problems involving consecutive supplementary angles:

Draw a diagram to visualize the problem.
Label all known angles and mark the ones you need to find.
Use the properties of consecutive supplementary angles to set up equations.
Always check your work to ensure accuracy.

With these strategies in your toolkit, you’ll be solving geometry problems like a pro in no time!

Advanced Concepts: Consecutive Supplementary Angles in Polygons

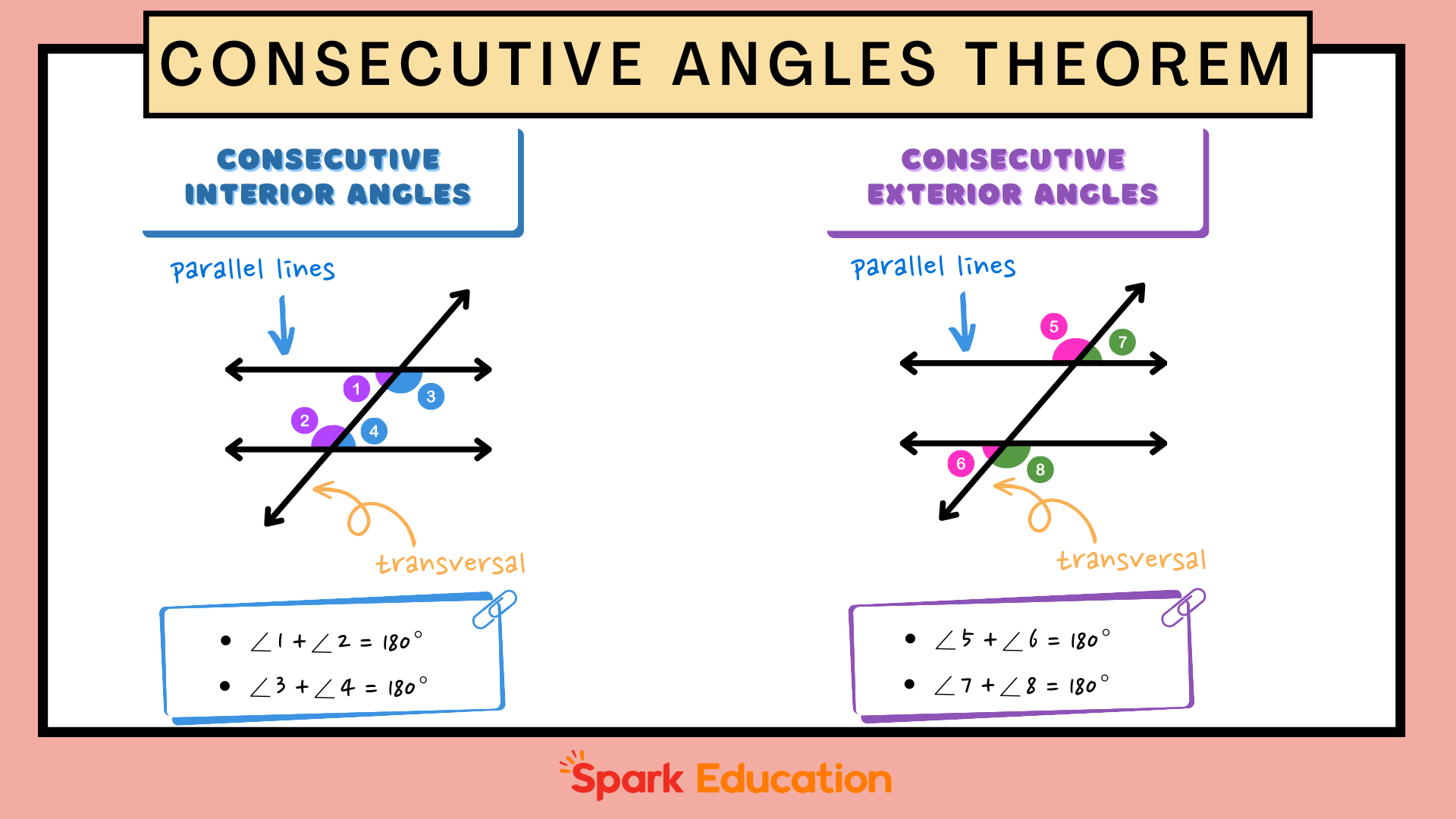
Once you’ve mastered the basics, it’s time to explore how consecutive supplementary angles apply to polygons. In a parallelogram, for instance, opposite angles are equal, and consecutive angles are supplementary. This means that if you know one angle, you can find all the others using these properties.

In trapezoids, the angles adjacent to each other along the same leg are also supplementary. This relationship can help you solve problems involving trapezoids, such as finding missing angles or determining whether a given figure is indeed a trapezoid.

Applications in Complex Shapes

When dealing with more complex shapes, such as irregular polygons, consecutive supplementary angles can still come in handy. By breaking down the shape into smaller parts, you can apply the same principles to solve for unknown angles. It’s like solving a puzzle – each piece fits together perfectly!

Consecutive Supplementary Angles and Linear Pairs

Linear pairs are another important concept closely related to consecutive supplementary angles. A linear pair consists of two adjacent angles whose non-common sides form a straight line. In other words, they are consecutive supplementary angles by definition.

Understanding the relationship between linear pairs and consecutive supplementary angles can simplify many geometry problems. For example, if you know that two angles form a linear pair, you automatically know that they are supplementary. This knowledge can save you time and effort when solving problems.

Key Differences Between Linear Pairs and Other Angle Pairs

While linear pairs and consecutive supplementary angles are similar, there are some key differences to keep in mind:

Linear pairs always form a straight line, whereas consecutive supplementary angles can appear in various configurations.
Linear pairs are a specific type of consecutive supplementary angles, but not all consecutive supplementary angles are linear pairs.

Recognizing these distinctions will help you apply the right concepts to the right problems.

Teaching Consecutive Supplementary Angles: Tips for Educators

For teachers and educators, explaining consecutive supplementary angles can sometimes be a challenge. Here are some tips to make the lesson engaging and effective:

Use real-world examples to illustrate the concept.
Encourage students to draw diagrams and label angles.
Provide plenty of practice problems to reinforce learning.
Use interactive tools, such as geometry software or apps, to make the lesson more dynamic.

By making the lesson interactive and hands-on, you’ll help students grasp the concept more easily and retain the information longer.

Resources for Learning and Teaching

There are many resources available to help both students and educators learn about consecutive supplementary angles. Websites like Khan Academy and Mathway offer tutorials and practice problems. Additionally, textbooks and workbooks dedicated to geometry can provide valuable exercises and explanations.

Conclusion: Embrace the Power of Consecutive Supplementary Angles

Consecutive supplementary angles might seem intimidating at first, but once you understand their properties and applications, they become an invaluable tool in your geometry arsenal. From solving basic problems to tackling complex shapes, these angles play a crucial role in the world of mathematics.

So, what’s next? Why not try solving a few practice problems or exploring how consecutive supplementary angles appear in your everyday life? And don’t forget to share this article with your friends and classmates – the more people who understand geometry, the better!

Remember, geometry isn’t just about numbers and shapes; it’s about seeing the world through a different lens. By mastering concepts like consecutive supplementary angles, you’ll not only improve your math skills but also gain a deeper appreciation for the beauty of mathematics.

Table of Contents:

What Are Consecutive Supplementary Angles?
Why Are Consecutive Supplementary Angles Important?
How to Identify Consecutive Supplementary Angles
Consecutive Supplementary Angles in Geometry Problems
Advanced Concepts: Consecutive Supplementary Angles in Polygons
Consecutive Supplementary Angles and Linear Pairs
Teaching Consecutive Supplementary Angles: Tips for Educators

A Complete Guide to Consecutive Angles in Geometry

Champions Of Knowledge